最近有一个需求,要对两段一维信号进行关键点匹配,所以来研究了下 Dynamic Time Warping 算法。这个算法简单来讲可以对两段近似但不一定等长的一维序列进行一对多匹配,并度量这两段序列的相似程度,算法的优化目标是匹配后的序列之间的距离最小。下面通过一些例子来详细说明一下。
问题背景
先考虑一个简单的问题,假设我们有两段等长的一维序列,我们如何度量他们的相似程度?一个简单的做法是直接作差计算欧几里得距离,例如:
1
2
a = [1, 2, 3]
b = [3, 2, 2]
它们的欧几里得距离是 $D=\sqrt{2^2+0^2+1^2}=\sqrt{5}$。这里面有一个假设,在作差的时候两个序列元素的位置是一一对应的,但有时这种方法不能反映两个序列直观的相似程度,例如对于序列:

这两个序列都包含一个相同的正弦波,直观来讲很相似,但如果直接作差会得到很大的距离。此外,有时也需要对不等长的序列进行计算,例如声音匹配,如果两个人同时说了 “Hello” 但快慢不同,应该也可以得到相对近似的结果。

对于这种序列,目前直接作差的方法也无法处理。我们需要一种方法,可以错位地对两个序列的元素进行匹配再作差,并且要能处理序列不等长的情况,这就是 Dynamic Time Warping。
问题描述
直接作差是对两个序列进行严格一对一的位置匹配,DTW 将这一条件放宽,即在两个序列中寻找一个一对多和多对一的映射,再作差求距离。我们假设两个序列分别为 s[0...n-1] 和 t[0...m-1],这种映射要满足一些限制条件:
- 两个序列中任意点都必须要在对方序列中有匹配点(可以重复)。
s[0]必须和t[0]匹配,s[n-1]必须和t[m-1]匹配。- 匹配序列必须单调递增,即如果存在两对匹配
(i, j)和(k, l)(i, k为序列s的下标,j, l为序列t的下标)且i<=k,则j<=l,且两个等号不同时成立。
在满足以上条件的所有映射中,使得两个序列差值最小的映射就是 DTW 算法的输出,相应的差值就是两个序列的 DTW 距离。
问题转化
问题定义已经清楚了,但满足 DTW 优化目标的映射如何用算法求解呢?我们先尝试转化一下问题,从以上问题描述中,我们不难有以下发现:
- 算法的目的在于寻找一个单调递增的匹配序列,这个序列的长度未知,但第一个元素一定是
(0, 0),最后一个元素一定是(n-1, m-1)。 - 因为序列中的每个点都要有匹配,所以匹配序列中两个相邻的元素的两对坐标要么同时差 1,要么仅有一个差 1,不能相差大于 1 的数。即,如果匹配序列中存在
(i, j),则它的下一个元素一定是(i+1, j), (i+1, j+1), (i, j+1)中的一个。 - 匹配后序列的差就是匹配序列中所有元素对的差值,我们要让这个差值最小。
这样一分析,问题就转化成了经典的最短路径问题:设想我们有一个 n * m 的棋盘,棋盘每个节点 (i, j) 的权重就是序列对应元素的距离 D(s[i], t[j]),我们要找到一条从 (0, 0) 到 (n-1, m-1) 的路径,使得路径经过的节点的权重之和最小。并且路径中每个节点只能在前一个的右侧、上侧或者右上侧。问题就转化成了一个经典的动态规划求最短路径问题,如下图所示:
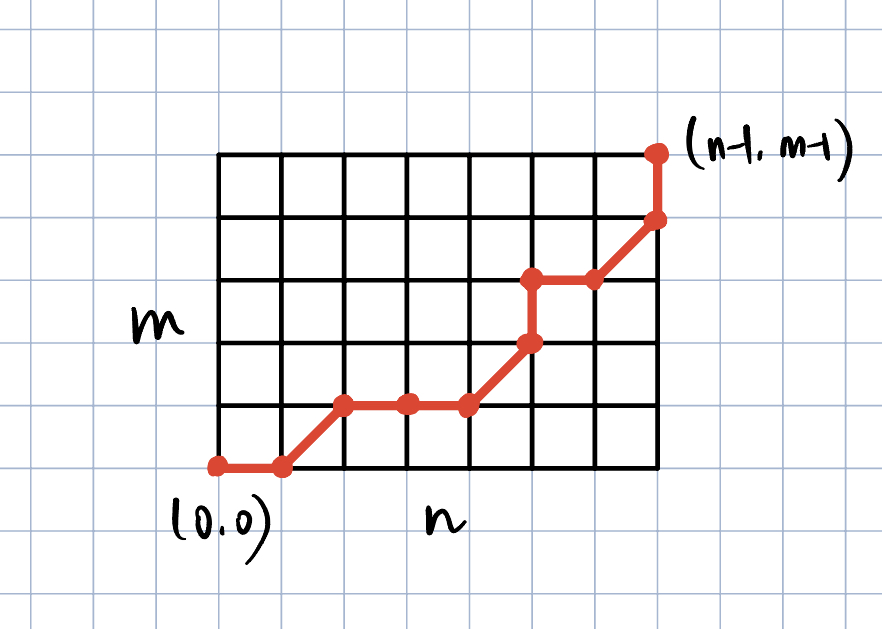
代码实现
动态规划求最短路径是一个经典算法,在此省略推导,直接给出状态转移方程: \(DTW(i,j) = Distance(s[i], t[j]) + min(DTW(i-1,j), DTW(i-1,j-1), DTW(i,j-1))\) 可用以下函数求出两段序列的 DTW 距离:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def dtw_dis_trivial(s:np.ndarray, t:np.ndarray) -> float:
''' Give two 1D sequences, calculate the dtw distance.
args:
s: np.ndarray, shape = (N,), the sequence 1.
t: np.ndarray, shape = (M,), the sequence 2.
returns:
float, the dtw distance.
'''
N, M = s.shape[0], t.shape[0]
dis_map = np.empty((N, M))
dis_map[0,:] = np.abs(t - s[0])
dis_map[:,0] = np.abs(s - t[0])
for i in range(1, N):
for j in range(1, M):
cost = np.abs(s[i] - t[j])
dis_map[i,j] = cost + min(dis_map[i-1,j-1], dis_map[i-1,j], dis_map[i,j-1])
return dis_map[N-1, M-1]
算法维护了一个二维距离矩阵,逐列更新每个点的最小距离,时间复杂度和空间复杂度均为为 $O(mn)$,可以压缩这个二位矩阵降低空间复杂度:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def dtw_dis(s:np.ndarray, t:np.ndarray) -> float:
''' Give two 1D sequences, calculate the dtw distance.
Use 1D DP vector to save space.
'''
N, M = s.shape[0], t.shape[0]
dis_vec = np.abs(t - s[0])
tmp1, tmp2 = 0, 0
for i in range(1, N):
tmp1 = dis_vec[0] + np.abs(s[i] - t[0])
for j in range(1, M):
cost = np.abs(s[i] - t[j])
tmp2 = cost + min(tmp1, dis_vec[j], dis_vec[j-1])
dis_vec[j-1] = tmp1
tmp1 = tmp2
dis_vec[M-1] = tmp1
return dis_vec[M-1]
这里的 dis_vec 仅存储了一行的数据,每次用 tmp1, tmp2 两个临时变量递推,空间复杂度降至 $O(m)$。
以上两个算法仅返回了 DTW 距离,如果要知道匹配关系,还需维护一个二维矩阵记录每个节点最小的前一个节点,最后从终点往前递推,如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
def dtw_match(s:np.ndarray, t:np.ndarray) -> Tuple[np.ndarray, float]:
''' Give two 1D sequences, calculate the dtw distance.
Also save and return how the two sequences match.
args:
s: np.ndarray, shape = (N,), the sequence 1.
t: np.ndarray, shape = (M,), the sequence 2.
returns:
Tuple[np.ndarray[(K,2),np.int32], float],
1st: the K matched index pairs;
2nd: the dtw distance.
'''
N, M = s.shape[0], t.shape[0]
dis_map = np.empty((N, M))
dis_map[0,:] = np.abs(t - s[0])
dis_map[:,0] = np.abs(s - t[0])
# record the min dis direction at each node (i, j),
# 0: invalid, 1: from (i-1, j), 2: from (i-1, j-1), 3: from (i, j-1)
dir_map = np.zeros((N, M), dtype=np.int32)
dir_map[0, 1:] = 3
dir_map[1:, 0] = 1
for i in range(1, N):
for j in range(1, M):
cost = np.abs(s[i] - t[j])
choices = [dis_map[i-1, j], dis_map[i-1, j-1], dis_map[i, j-1]]
idx = np.argmin(choices)
dir_map[i,j] = idx + 1
dis_map[i,j] = cost + choices[idx]
# trace back the matched index pairs
s_idx, t_idx = [N-1], [M-1]
while True:
i, j = s_idx[-1], t_idx[-1]
dir = dir_map[i, j]
assert dir != 0
if dir == 1 or dir == 2: i -= 1
if dir == 2 or dir == 3: j -= 1
s_idx.append(i)
t_idx.append(j)
if i == 0 and j == 0: break
return np.column_stack([s_idx, t_idx])[::-1,:], dis_map[N-1, M-1]
这就是 DTW 的完整算法,我们可以构造两个有噪声的相似的正弦函数来检验算法给出的匹配是否合理:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
if __name__ == '__main__':
np.random.seed(0)
N, M = 60, 50
x1 = np.linspace(0, 2*np.pi, num=N)
x2 = np.linspace(0, 2*np.pi, num=M)
y1 = np.sin(x1) + 0.1 * np.random.randn(N)
y2 = np.sin(x2) + 0.1 * np.random.randn(M)
pairs, dis = dtw_match(y1, y2)
gap = 2
for s, t in pairs:
plt.plot([s, t], [y1[s]+gap, y2[t]], color='black')
plt.plot(y1 + gap, linewidth=3)
plt.plot(y2, linewidth=3)
plt.show()
匹配结果如下:
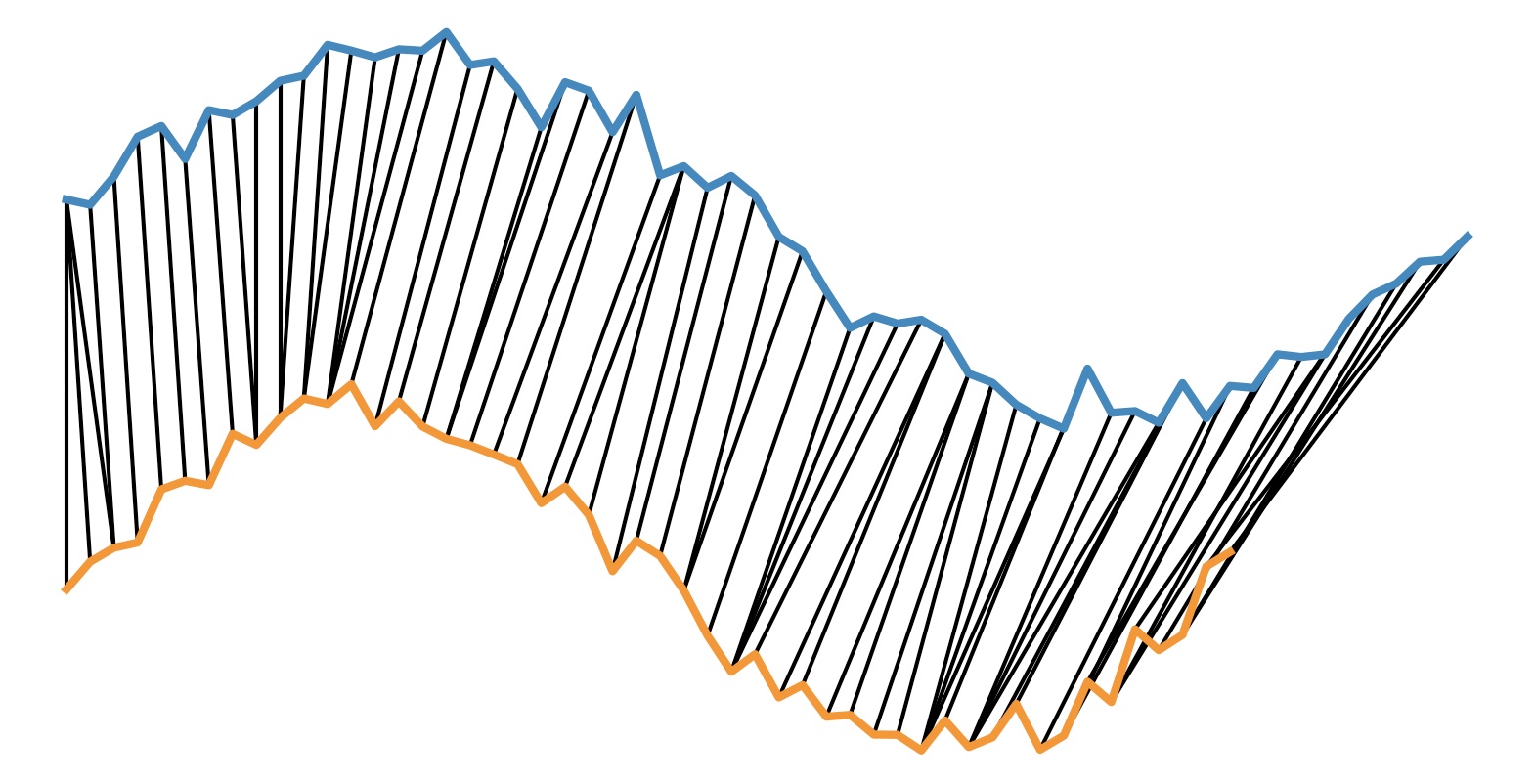
可以看出匹配的结果还不错,两个正弦函数相似的部分大致被匹配到了一起。除此以外,以上算法用 python 实现运行比较慢,还可以借助 fastdtw 库,在 $O(n)$ 的时间复杂度内得到近似的 DTW 匹配:
1
2
3
4
5
6
7
8
9
from fastdtw import fastdtw
def dtw_match_fastdtw(s:np.ndarray, t:np.ndarray) -> Tuple[np.ndarray, float]:
''' Give two 1D sequences, calculate the dtw distance.
Also save and return how the two sequences match.
Implement based on package fastdtw.
'''
dis, path = fastdtw(s, t)
return np.array(path, dtype=np.int32), dis
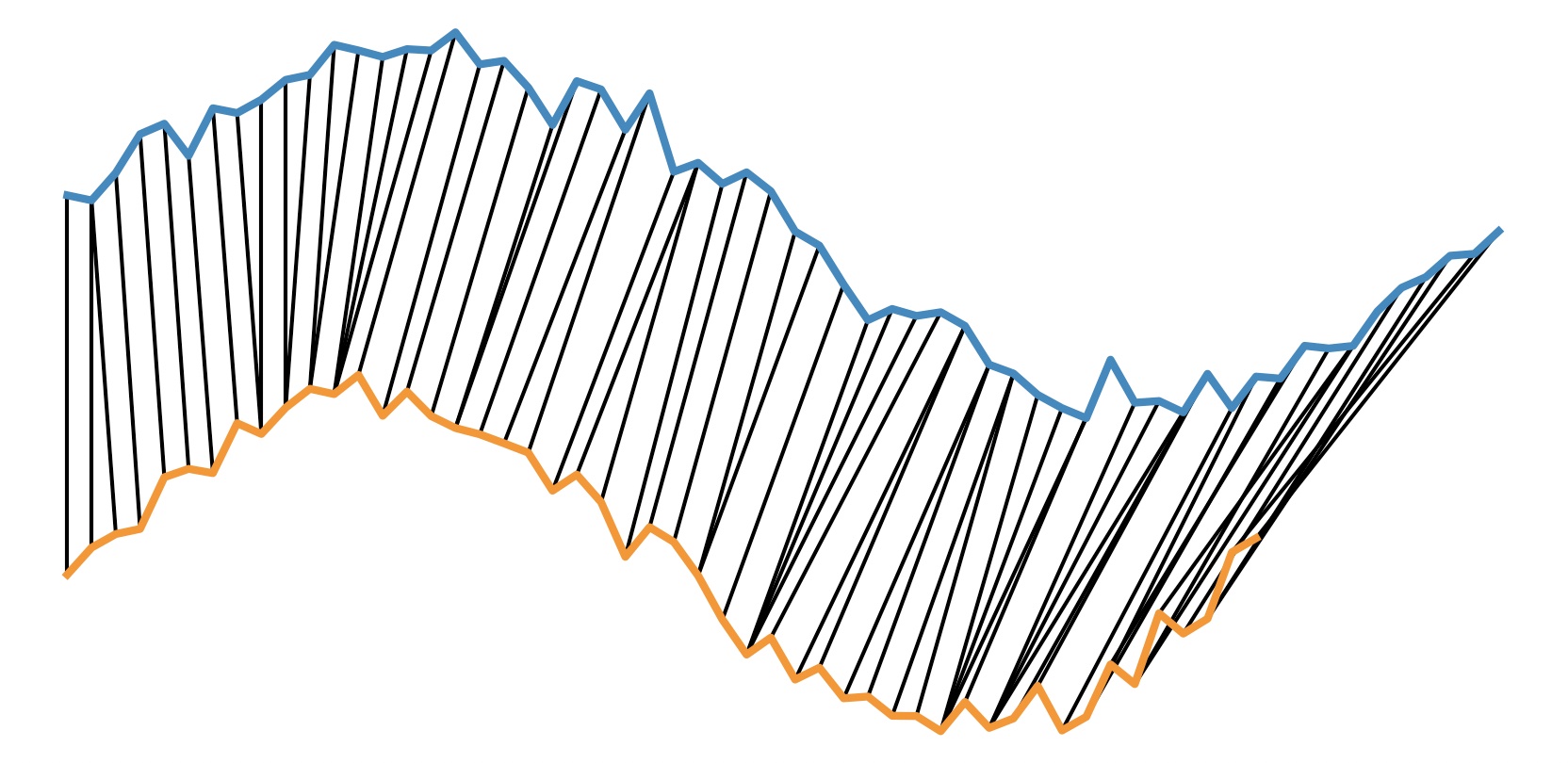
fastdtw 的结果和严格的 DTW 有一些微小区别,但效率会高很多,在绝大多数时序信号匹配的场合已经很够用了。
以上就是 DTW 从数学原理到代码实现的全部内容了。DTW 在实际使用时还有一些变体,例如限制在某一个窗口大小内进行匹配,相当于把棋盘的左上角和右下角砍掉进行路径搜索,本质的原理还是一样的。希望这篇笔记对你有所帮助 :)
参考资料
- 维基百科:https://en.wikipedia.org/wiki/Dynamic_time_warping
- 一篇 DTW 的教程:https://towardsdatascience.com/dynamic-time-warping-3933f25fcdd
- fastdtw 库:https://pypi.org/project/fastdtw/