概述
- Allan Variance 用来定量描述电子器件测量误差和平均时间的关系。
- 假设测量值是一个常量 + 随机噪声,取多次测量值的平均作为一次测量值可以减小随机波动的方差。
- 但若测量值不是常量,有一个较小的漂移,则随平均次数的增大方差反而会增大。
- 一般的 Allan Variance 曲线是一个下凸函数,可以用来寻找最合适的平均次数,也可以分析传感器的各类型误差特征。
Signal Averaging for Noise Reduction
理想情况
- 假设要测量直流电流信号,电流是常量,但测量值有随机波动,测量信号为 $\hat{I}(t) = I_0 + z(t)$。
- 其中 $z(t)$ 是随机噪声,$Var(z(t)) = \sigma_n^2$。
- 每次只测量一次,则测量误差 $E_{I}(1) = Var(\hat{I}(t)) = Var(z(t)) = \sigma_n^2$。
- 测量 M 次取平均,误差减小为 $E_{I}(M) = Var(\sum_{i=1}^{M}\cfrac{z(Mn+i)}{M}) = \cfrac{\sigma_n^2}{M}$。
- 在 log-log 空间 $log(E_{I}) = 2log(\sigma_n) - log(M)$,是一条斜率为 -1 的直线,平均次数越多误差越小。
测量信号有漂移
- 假设测量信号有一个线性漂移,$\hat{I}(t)=I_0+\alpha t+z(t)$。
- $\alpha$ 是一个很小的常量,$z(t)$ 是随机噪声 $Var(z(t)) = \sigma_n^2$。
- 测量 M 次取平均,经过一些数学推导可得测量误差 $E_I(M) = Var(\hat{I}(t)) = Var(\alpha t) + Var(z(t)) = \cfrac{\sigma_n^2}{M} + \cfrac{\alpha^2\Delta t^2M^2}{12}$。
- $\Delta t$ 是测量间隔,可见误差先减小后增大,$M=\sqrt[3]{\cfrac{6\sigma_n^2}{\alpha^2\Delta t^2}}$ 取得最小值。
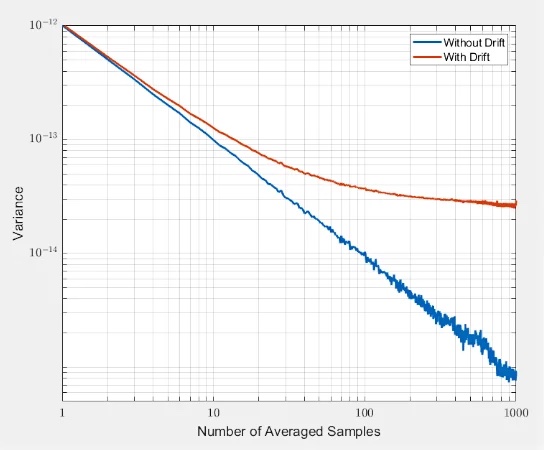
- 下图展示了有无漂移时的 Allan Variance 曲线:
Non-overlapping Allan Variance
- 一个时间窗口取平均出一个测量值,时间窗口不重叠。
- 公式为 $\sigma^2(T) = \cfrac{1}{2(K-1)}\sum_{k=1}^{K-1}(\bar{\Omega}{k+1}-\bar{\Omega}{k}(T))^2$。
- 一共 $N$ 个点,分成 $K$ 个窗口,每个窗口 $n$ 个点,一个窗口时间 $T=n\Delta t$。
Overlapping Allan Variance
- 一个时间窗口出一个测量值,时间窗口紧密重叠,错开一个间隔。
- 公式为 $\sigma^2(T)=\cfrac{1}{2(N-2n+1)}\sum_{k=1}^{N-2n+1}(\bar{\Omega}_{k+n}(T)-\bar{\Omega}_k(T))^2$, 符号含义同上。
Typical Allan Deviation Plot
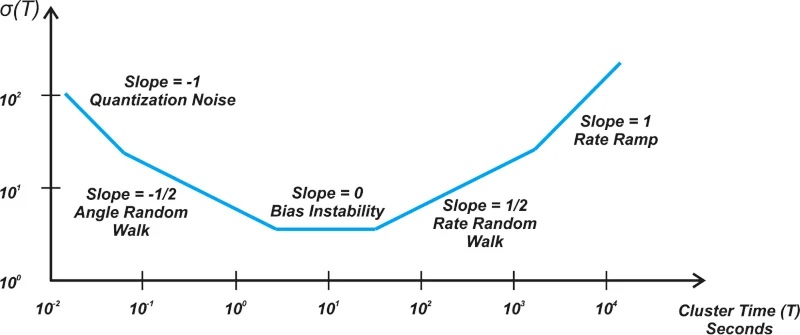
- 平均次数取一个中间的合适值达到最小测量误差。